A (not so) safe betting strategy for winning at roulette
A couple of years ago I was on a trip to Budapest with a couple of friends. While roaming the streets we were passing by a casino and my friend insisted that there was a perfect strategy that would only lead to winning at roulette tables. Curious as I was I had him explain his theory. The system basically works as follows:
First, you place a coin on red. If red wins, take your winning and start over. Otherwise, you double your bet after every loss, so that the first win would recover all previous losses plus win a profit equal to the original stake. If there were no constraints this could actually work. I usually get suspicious when I hear “guaranteed wins” in the context of gambling. My first doubt was, that the chance of getting either red or black were not equally fifty percent since there was also the zero. Another thing is that at a roulette tables there is usually a limit.
I thought the best way to convince my friend that his system was not so perfect as he thought, was to simulate the whole process and show him the outcome.
Our gambler starts with a budget of 1000 coins and bets 1 coin initially. He also has a winning target, that if he reaches it, he withdraws from the table and goes home happily. The table limit is 1200 coins per bet. For simplicity I also assume that if zero comes up it counts as a lost bet.
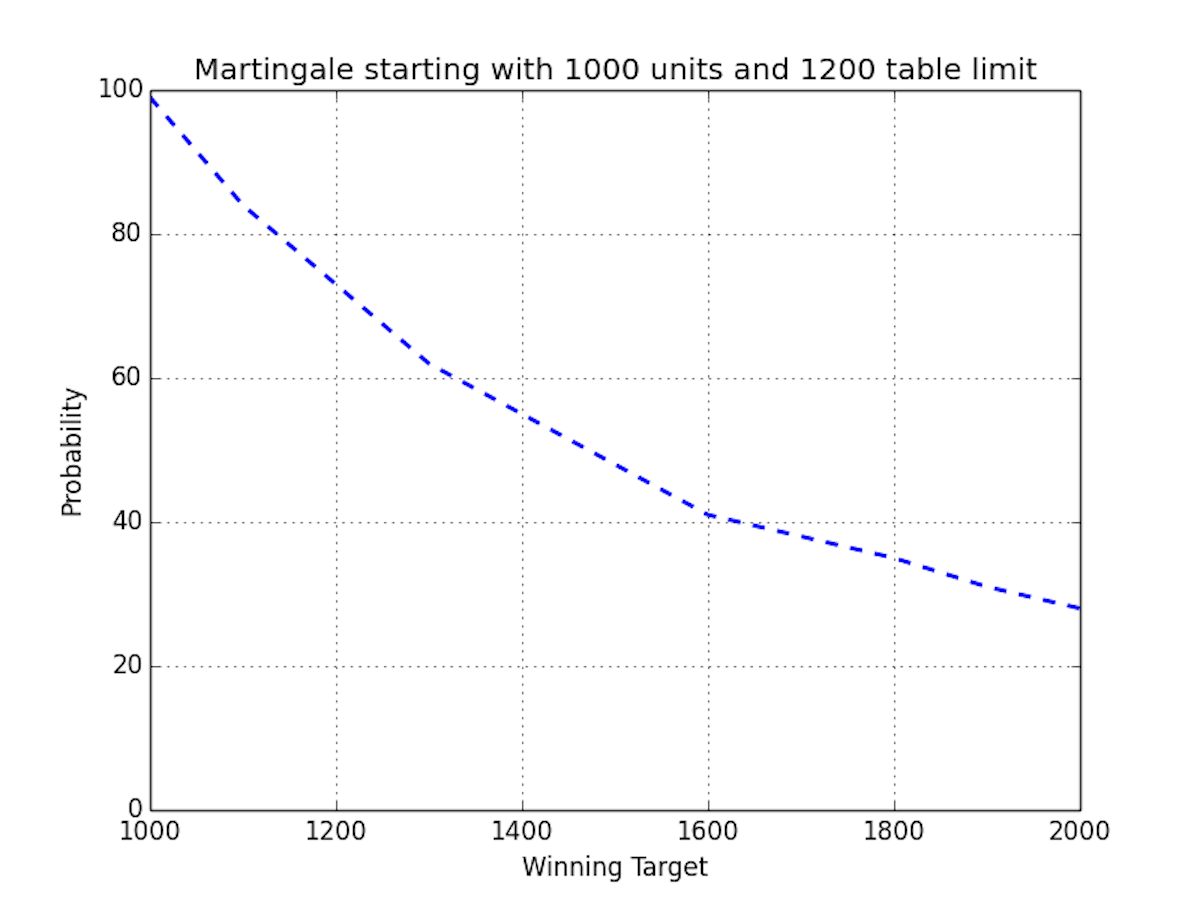
The graph shows clearly that the higher the gambler sets it target the lower is the probability of reaching it. If you want to play with the system, alter some parameters or extend it to a different betting strategy here is my code:
| #!/usr/local/bin/python | |
| # encoding: utf-8 | |
| import random | |
| import time | |
| import matplotlib.pyplot as plt | |
| import numpy as np | |
| #simulates the martingale roulette system | |
| def simulation(): | |
| print("Here we go") | |
| # maximum money you can put on the table | |
| limit = 1200 | |
| #rounds of games simulated | |
| rounds = 10000 | |
| #get time stamp | |
| before = time.clock() | |
| #simulates games up to the target of 1000..2000 units by 100 | |
| x, y = [], [] | |
| for i in xrange(1000, 2001, 100): | |
| print(i) | |
| won = 0 #games won | |
| for j in xrange(1, rounds): | |
| target = i #if reached target => success | |
| money = 1000 # inital money | |
| bet = 1 #inital bet | |
| while True: | |
| if (money >= target): | |
| won += 1 | |
| break | |
| number = random.randrange(0, 37) # Rien ne va plus! | |
| if (number == 0): # zero always loses | |
| money -= bet | |
| bet *= 2 | |
| else: | |
| if (number % 2) == 0 :# even number == round won | |
| money += bet | |
| bet = 1 | |
| else: # odd number == round lost | |
| money -= bet | |
| bet *= 2 | |
| if (bet > money): # put in all you have | |
| bet = money | |
| if (money <= 0): # poor you | |
| break | |
| if (bet > limit): # cannot go over the limit | |
| bet = limit | |
| #compute statistics | |
| lost = rounds - won | |
| ratio = (100*won/rounds) | |
| x.append(i) | |
| y.append(ratio) | |
| # chart says more than a thousand words | |
| x, y = np.array(x), np.array(y) | |
| line, = plt.plot(x, y, '--', linewidth=2) | |
| plt.xlabel('Winning Target') | |
| plt.ylabel('Probability') | |
| plt.title('Martingale starting with 1000 units and 1200 tabel limit') | |
| plt.ylim(ymin=0) | |
| plt.grid() | |
| plt.show() | |
| print('Target: %d, Games won: %d, Games lost: %d, Ratio: %f' % (target, won, lost, ratio)) | |
| elapsed = time.clock() - before | |
| print("%d rounds took %d seconds" % (rounds, elapsed)) | |
| def main(): | |
| #start the simulation | |
| simulation() | |
| if __name__ == '__main__': | |
| main() |